To attain tritium self-sufficiency, one of the most promising EU DEMO design concepts includes Breeding Blanket (BB) with liquid Lead-Lithium Eutectic (LLE) alloy as a coolant and/or tritium breeder. Tritium is produced through neutron capture (nuclear) reactions by lithium isotopes in LLE. The LLE is preferred over pure liquid lithium for safety purposes.
In the course of nuclear breeding reactions of tritium, helium is produced in the same amount (number of moles) as tritium. The extreme low solubility of helium in LLE has triggered the concerns of a potential nucleation issue that would drastically affect the major design parameters of the BB, which include: (1) MHD pressure drop, (2) heat transfer coefficient, (3) tritium permeation, and (4) tritium inventories. Furthermore, being LLE an electrically conductive liquid metal (LM), it will present Magneto-Hydro-Dynamic (MHD) effects under the magnetic field used to keep the plasma in place. Accordingly, these effects will modify the velocity profiles and the heat and mass transfer characteristics of tritium.
The little-known behaviour of two-phase gas-liquid metal flow coupled with MHD effects results in an acute lack of correlations for the BB design parameters. Under this scenario, numerical simulations with system codes or 1D models cannot accurately capture the complexity of the flow. Experimental studies of BB in relevant working conditions are technologically challenging and require costly research efforts. Alternatively, CFD models appear as powerful and flexible tools to investigate the trends of the design parameters and obtain the necessary correlations to help BB system designers make decisions. In this sense, CFD models developed by our group have been successfully used to describe MHD phenomena [1,2], helium nucleation [3,4], and tritium transport [5] in fusion reactor blankets. Using these models, we have found, for instance, the influence of design variables on the parameter that defines the heat transport (Nu, Nusselt number) (Figure 1):

Figure 1. Dependence of Nusselt number on the fluid velocity (Re), the magnitude of thermal deposition (Gr), and magnetic field intensity (Ha) [2].
The previous approximation to the transport correlations has been obtained for single-phase liquid metal flows. However, there are two scenarios in which coupled MHD/gas-liquid metal two-phase flows are relevant in a BB: 1) a pressurized helium leak into the LM due to a loss of coolant, and (2) the presence of nucleated bubbles originating due to the high helium production rates, relatively low pressures, and long LM residence times.
The interaction of gas-liquid metal two-phase flows with a magnetic field has attracted the attention of researchers for the last 60 years. Most of the studies in the literature are devoted to the investigation of flow regimes relevant for accident scenarios such as those involving a pressurized helium leak into the LM. Studies relevant to normal operating conditions (i.e., nucleated He bubbles into the LM) are scarce and inconclusive due to the lack of experiments and simplified approaches. The appearance of nucleated He bubbles influences the path of the electric currents that govern the MHD phenomenon and the tritium transport. Thus, it is important to study, on a microscopic scale, the mechanisms of bubble formation by atomistic simulations and, on a macroscopic scale, the interaction of the He/LLE flow with a magnetic field.
Atomistic simulations of helium nucleation in liquid metals
The ANT and SIMCON research groups at UPC have established a multi-level multi-approach project to investigate the helium nucleation in LLE-BB rigorously using state-of-the-art theories and tools. Aiming to resolve main issues and concerns in the associated research in the past, Molecular Dynamics (MD) has been selected as a cornerstone in the methodology, and it is referred to as atomistic simulations. MD methods rely on statistical physics to describe the atomistic nature, properties and behaviour of matter and phases. In essence, MD methods are used to describe the liquid state of the system (helium in LLE). Statistical thermodynamics allows to bridge between “nanoscopic” and macroscopic properties. For example, atomistic simulations are capable of reproducing experimental thermophysical properties of LLE such as density, heat capacities, melting points, surface tension, etc.
Of course, the aforementioned capabilities require a reliable and accurate input to describe the atomistic interactions. The main input, and usually unknown or uncertain, is the interatomic potential that governs how two atoms (e.g., Lennard-Jones potential) or a group of atoms (Many-Body potential) interact with each other. Currently, the project is divided into modules using different approaches (ab initio calculation, Lennard-Jones, Many-Body potentials, theoretical estimations) with hierarchical verification and validation procedures. This is due to the complexity of the system being investigated, scarcity of counterpart experimental data and the limited validity of many relevant theories.
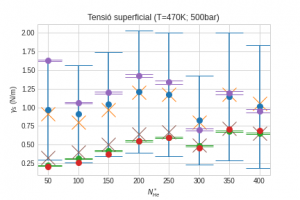
As an example, Figure 2 shows the surface tension as a function of the number of helium atoms in a bubble at two temperatures. Different methods were considered: (a) Thompson’s method [6] (blue and orange crosses) considers an atomistic point of view, taking into account the normal component of the pressure, although spherical symmetry and mechanical equilibrium need to be assumed; (b) the classical Young-Laplace equation (green and red dots, with pressures calculated directly from the simulation – virial theorem and the Hurly-Moldover equation of state [7], respectively) estimates surface tension, but cannot be accurate in the nano-scale; (c) similarly, brown crosses use the capillarity equation; (d) purple points represent the ratio between the cohesive energy of bubbles (as an estimation of their work of formation) and their surface area.
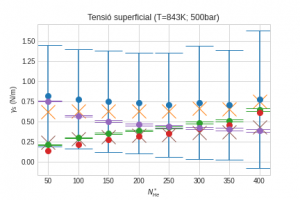
Figure 2. Surface tension (in liquid lithium) vs number of helium atoms of bubbles at temperatures of 470 K (bottom up) and 843 K (bottom down).
For heavy liquid metals and alloys such as LLE, the Embedded Atom Method (EAM) potentials are more accurate in describing atomistic interaction due to their high density (packing of atoms) and complex electronic structure. This part of the project is complemented with “ab initio” calculations aimed at obtaining important parameters, such as liquid structure, that are neither available from experimental databases nor can be obtained experimentally.
The capability of reproducing coexistence of phases (e.g. solid/liquid, liquid-gas, etc.) in equilibrium using atomistic simulations is the main motivation behind their deployment in predicting nucleation and solubility of helium in LLE. As a simple illustration, Figure 3 depicts the application of melting-point estimation of pure lithium, which is estimated at 457 K (experimental melting point is 454 K). This technique relies on obtaining a thermodynamically-stable simulation of liquid and solid lithium phases with two interfaces. The results are obtained using a mixed EAM potential to represent pure liquid Li and LLE that has been developed by ANT group for the project purposes, and with enhancements over those found in literature.

Figure 3. Solid/Liquid lithium atoms in coexistence and thermodynamic equilibrium. The temperature at which the system relaxed represents the melting-point estimation. Green atoms are in the liquid phase (note the random ordering) and blue atoms are in solid phase (note the systematic ordering as per the BCC structure of solid lithium).
CFD simulation of gas/liquid metal flows
To simulate (on a macroscopic scale) the dynamics of helium bubbles and their mass transfer behaviour in LLE, CFD models are being developed and validated using the data available in the literature. The initial calculations, to test the models, have been done using argon and galinstan as reference fluids. Inputs, assumptions and boundary conditions used in the present study are essentially the same as the ones used by Miao et al. [8]. Figure 4 shows the computational domain and a typical mesh applied in its discretization. The problem under consideration consists of the injection of gas bubbles into a pool with a liquid metal (being at rest without gas flow) through a single orifice located at the centre of the container bottom. The fluid container is situated within a homogeneous DC magnetic field, which can be aligned in either vertical (longitudinal) or horizontal (transverse) direction.

Figure 4. Computational domain and exemplary mesh used for the simulations.
Figure 5 illustrates the influence of the magnetic field on the bubble volume fraction and the spatial distribution of the liquid metal velocity. The tendency of the flow to align with the magnetic field can be observed. Also shown in Figure 6 are some preliminary results for the radial distribution of the liquid vertical velocity. The similarities between the reference and obtained profiles can be observed. Moreover, the influence of several parameters, such as bubble diameter and magnetic field, has been also investigated, as illustrated in the figure to the right.
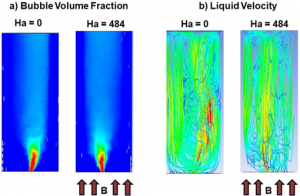
Figure 5. Influence of a longitudinal magnetic field on gas-liquid metal two-phase flows.
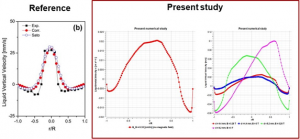
Figure 6. Liquid vertical velocity profiles in the radial direction at the mid-height of the liquid metal column: (left) reference profile ([8]); (centre) simulated profile; (right) influence of different experimental conditions (bubble diameter and magnetic field).
ANT and SIMCON research groups at UPC are coordinating efforts in the investigation of the helium nucleation phenomenon in the metal liquid circulating in the breeding blankets of a future fusion nuclear reactor. Molecular Dynamics is at the centre of the methodology.
ANT is also investigating the simulation of two-phase flows (helium bubbles in lead-lithium eutectic) in fusion reactor relevant conditions.
Results obtained are promising and work is continuing at good pace.
References
[1] E.M. De Les Valls, L. Batet, V. De Medina, J. Fradera, L. Sedano, Modelling of integrated effect of volumetric heating and magnetic field on tritium transport in a U-bend flow as applied to HCLL blanket concept, Fusion Eng. Des. 86 (2011) 341–356. doi:10.1016/j.fusengdes.2011.02.075.
[2] D. Suarez, E. Iraola, C. Lampón, E. Mas de les Valls, L. Batet, Liquid metal MHD flow influence on heat transfer phenomena in fusion reactor blankets, Fusion Eng. Des. 170 (2021) 112503 (10 pp). doi:10.1016/j.fusengdes.2021.112503.
[3] L. Batet, J. Fradera, E.M.D. Les Valls, L.A. Sedano, Numeric implementation of a nucleation, growth and transport model for helium bubbles in lead-lithium HCLL breeding blanket channels: Theory and code development, Fusion Eng. Des. 86 (2011) 421–428. doi:10.1016/j.fusengdes.2011.03.074.
[4] J. Fradera, L. Sedano, E. Mas De Les Valls, L. Batet, Implementation of two-phase tritium models for helium bubbles in HCLL breeding blanket modules, J. Nucl. Mater. 417 (2011) 739–742. doi:10.1016/j.jnucmat.2011.02.008.
[5] L. Batet, E. Mas De Les Valls, L.A. Sedano, Mathematical models for tritium permeation analysis in liquid metal flows with helium bubbles, Fusion Eng. Des. 89 (2014) 1158–1162. doi:10.1016/j.fusengdes.2014.04.031.
[6] S. Thompson, K. Gubbins, J. Walton, R. Chantry, and J. Rowlinson, A molecular dynamics study of liquid drops,The Journal of chemical physics 81, 530 (1984). doi:10.1063/1.447358
[7] J. J. Hurly and M. R. Moldover, Ab initio values of the thermophysical properties of helium as standards,Journal of research of the National Institute of Standards and Technology 105, 667 (2000)
[8] X. Miao, D. Lucas, Z. Ren, S. Eckert, G. Gerbeth, Numerical modeling of bubble-driven liquid metal flows with external static magnetic field, Int. J. Multiph. Flow. 48 (2013) 32–45. doi:10.1016/j.ijmultiphaseflow.2012.07.014.