Introduction
The development of new Tokamak concepts based on a very high magnetic field gives rise to the possibility of a new generation of compact systems and creates the opportunity to approach a new family of fusion systems beyond the state of the art and, with it, to start the transition from huge machines to smaller systems compatible with concepts such as distributed generation and with less impact on the environment.in addition to the conceptual evolution of elements towards new options of fusion systems, such as “liquid blanket” for example, it is necessary to introduce new materials and new technologies for the construction of suitable magnets that allow obtaining sufficiently intense magnetic fields, in the range of 20T [1]. The quality of the cables based on Low Temperature Superconductors (LTS) is very high, as well as the coils based on them [2] but the LTS materials are one of the limiting factors to achieve the values of flux density required by the new generations of smaller compact reactors of less cost and less environmental impact.The development of so-called high temperature superconductors (HTS) has made it possible to produce magnets of up to 45.5T [3], while LTS cables cannot reach the superconducting state in fields higher than 19 T. The development of wiring for magnetic coils HTS with HTS cables is now one strategic participant more in the fusion race which has included new players, at less two private companies (Commonwealth Fusion Systems and Tokamak Energy) plan to build the first compact plant by 2035. Compact fusion plants are expected to supply 0.5 GW in a modular configuration that allows for flexible territorial distribution.
New designs require new tools. HTS-based cables and coils require a specific computation environment in regards to their properties and performance from a mechanical, thermal or electromagnetic point of view.
The collaboration between BSC and ICMAB has begun to build a new computing module for the ALYA [5] platform that allows the possibility of facing the multiphysics problems that the design of coils for Fusion needs. In a first stage, the development of an electromagnetic module that allows the 2D and 3D computation of the current density distribution in the HTS cable has been undertaken, taking into account its specific architecture and working conditions. The problems related to the magnetization of the HTS conductor by external field and by the electric current itself have been solved and tested with the existing and published benchmarking results [4] as well as with solutions obtained by the ICMAB group using COMSOL. In this context of collaboration, BSC has developed the “Magnet” module on the experimental bases carried out by ICMAB, emphasizing the inclusion of adequate resources to solve the problems presented by HTS in the design of magnets of Tokamak. The module contemplates the ability to include mechanical and thermal aspects, already existing in the ALYA environment, giving rise to a highly useful multiphysics tool. The project includes the design of physical tests for validation of the calculation by using Hall Magnetometry and losses analysis performed by ICMAB. Less complex problems are solved using COMSOL to contrast the results with those obtained by the “Magnet” module.
The ALYA’s MAGNET module for HTS computation
In this first stage, the HTS module has been developed to solve the H formulation, for low frequency, of the Faraday equation (ec1), and assuming that the HTS materials behave according to the non-linear equation (equation 3).
𝜇0 ∂H/∂t + rot(𝜌 J)=0 (eq. 1);
J = rot(H) (eq. 2);
𝜌=Ec/Jc (J/Jc)n-1 (eq. 3);
This formulation speaks directly in terms of the essential quantities involved in typical superconducting engineering problems: magnetic field (H) and electric current density (J). It also includes the physical properties of the material involved, such as Jc (critical current) and “n”, values both measured and supplied by the manufacturer. Ec marks the electric field obtained when J = Jc. The value of Ec = 10-4V/m is conventionally accepted.
Although eq1 allows us to solve the electromagnetic problem, the condition div (H) = 0 could occasionally be explicitly included using a Lagrange multiplier to avoid the possible incompatibility of an overdetermined system.
Modelling HTS tapes
Conductors for braiding and making high-critical temperature superconducting cables are commercially available as tapes 30-100 microns thick and 2-12 mm wide. In these tapes, only a 1-3 micron layer corresponds to the textured HTS ceramic, with its crystalline structure oriented along the entire tape (fig 1). This tape architecture introduces a difficulty in calculating the actual values of the current density in this layer. The large difference in scales between the HTS layer and the full size of the tapes leads to the so-called “homogenization”. This simplification means that current can flow through the entire thickness of the tape, being Jc the complete critical current (Ic) divided by the area of the section of the tape. The effect of this assumption can only be seen on the thickness scale, but not when the coil assembly is considered, on a much larger scale. In case of a local event, such as a hot spot leading to a quench, the analysis performed on the tape thickness scale makes sense to consider the internal architecture of the superconducting conductor.

Fig 1 From tapes to cabling for magnets: transposition approaches Röbel, CORC, Twisting,
HTS tapes characterization
The values of Jc and “n” are essential for the modeling of HTS systems, with Jc being the most critical. “n” has a lower impact and is normally considered in the range of 20 to 30. However, in the case of Jc, this value has a great impact on the behavior of the HTS material, the values of Jc = 2×108 A/m2 they are typical in the homogenized field, common in HTS engineering. This parameter is not a constant, it depends on the temperature (T), the magnetic field (H) and also on the strainn (ε) due to the mechanical conditions in which the superconductor works. Furthermore, the direction (α) of the external magnetic field in which the superconductor operates, in relation to the orientation of the crystalline HTS ceramic also modifies the value of Jc due to the anisotropy of the lattice of the HTS crystals. Manufacturers provide the values of Jc as a function of B, T and α, the dependence on mechanical deformation is indirectly provided as maximum critical stress, which is the mechanical stress at which Jc decreases by 5%. The measurements of this unit are carried out by some Research Laboratories. ICMAB can perform this characterization under a magnetic field of up to 9T at temperatures up to 5K. It is currently building a new facility to reach 16T, which brings its capacity closer to the levels necessary for the study of accelerators and compact Tokamaks.
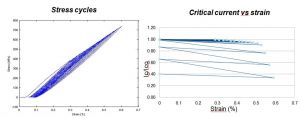
Fig 2 Right: Critical current dependence of Mechanical conditions for an HTS tape, irreversible behavior is detected for strain larger than 0.5%. Left: standard behavior in fatigue tests (ICMAB), measurements have been made at 77K.
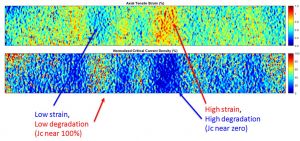
Fig. 3 Dependence of Jc with the deformation in a taut HTS tape, the local fall of Jc correlates with the local deformation measured by ICMAB by means of digital correlation of image and scanning Hall microscopy (ICMAB)
Results validation
The application of an external magnetic field on an element with zero resistance leads to a perfect shielding of the field, the system does not allow the penetration of the field in its volume. HTS (Type II) materials have a limit for the current density, the critical current density, which allows the field to enter but, when the applied field is removed, the field within the HTS material remains partially, only the one known as trapped field. This trapped field corresponds to the persistent currents induced in the material, the field of critical current density. The distribution in the field presents the local values of the critical current. The measurement of the perpendicular component of the trapped field can be carried out on the surface of the tape after being subjected, until saturation, to an external magnetic field using a Hall probe that sweeps the surface [6]. The magnetic field map obtained allows the calculation of the local value of the critical current. This distribution makes it possible to compare with results obtained through modeling or to obtain the values necessary for modeling. This procedure can be performed on tapes through which current circulates in order to determine how it is distributed (Fig4).
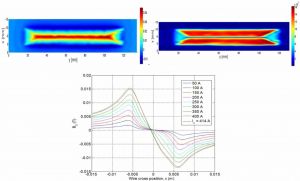
Fig4. Above: map of the trapped field after magnetizing with an outer field. Right: map of local critical currents. Down. Transverse distribution of Bz on the surface of an HTS tape through which current flows. The measured values allow comparison with the results of the models (measured by ICMAB)
Magnetic characterization using scanning Hall microscopy [6] is powerful enough to compare the experimental results with those of the simulation with the Magnet module developed by BSC. In the second stage, we are developing complementary experimental validation mechanisms of the HTS system. Among the most important values in a system based on superconductors is the value of the power losses. It is a critical value for design of the cooling system. The energy losses in a superconductor are due to the energy invested in the formation of the internal magnetic field of the superconductor during the charging and discharging processes. In the regime of change of the magnetic field, an electric field E is produced due to the variation of flux. The dot product J.E is a power density and the integral extended to the entire volume of the superconductor constitutes the energy loss per unit time during the change cycle. Modeling allows the calculation of losses and its measurement allows its experimental validation. Its measurement can be carried out in two ways. A thermal path, which measures the heat emitted in the cryogenic system and an electrical path, which measures the real component of the impedance. Both measurement systems are under development at ICMAB. The validation process of the new ALYA module refers, comparing with existing solutions, both to solving the problem in a reduced dimension using COMSOL and to contrasting it with significant experimental values. Figure 5 shows the losses per meter and cycle of a 12 mm wide HTS tape when it carries an alternating current of 50Hz of 100 A to 800 A, being Ic = 400A. The calculation of losses in a loop or non-cylindrical coil (problem 3D) is within the scope of ALYA’s options.
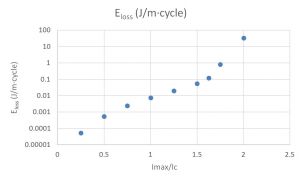
Fig 5 Losses in an tape carrying AC current (50 Hz) as a function of the current. Calculation carried out with COMSOL by ICMAB and contrasted with the benchmarking values offered by HTS Modeling Working group [4]. Of note is the change of regime when the current exceeds the critical value, at which the Joule losses prevail.
[1] A review of commercial high temperature superconducting materials for large magnets: from wires and tapes to cables and conductors. D Uglietti; Superconductor Science and Technology, Volume 32, Number 5, April 2020
[2]Limits of NbTi and Nb3Sn, and Development ofW&R Bi–2212 High Field Accelerator Magnets A. Godeke, D. Cheng, D. R. Dietderich, P. Ferracin, S. O. Prestemon, G. Sabbi, and R. M. Scanlan. eScholarship Open Access Publications from the University of California (2008)
[3] 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet. Seungyong Hahn, Kwanglok Kim, Kwangmin Kim, Xinbo Hu, Thomas Painter, Iain Dixon, Seokho Kim, Kabindra R. Bhattarai, So Noguchi, Jan Jaroszynski & David C. Larbalestier; Nature volume 570, pages496–499(2019)
[4] HTS numerical modelling workinggroup— www.HTSmodelling.com Benchmarking
[6] Magnetic mapping, a way to test and understand current flows in thin and bulk superconductors . Granados X, Iliescu S, Bozzo B, Bartolome E, Puig T, Obradors X, Amoros J, Carrera M. https://doi.org/10.4028/www.scientific.net/AST.47.1

